Graphs §

---

A graph consists of:

• A set of fixed objects, nodes.
• A set of edges, which may have arrows and have values attached.

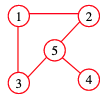
A graph $G=(V,E)$ is composed of:

• $V$: set of vertices or nodes.
• $E$: set of edges or lines connecting the vertices in $V$.
• An edge $e=(u,v)$ is a connection between the vertices $u$ and $v$.

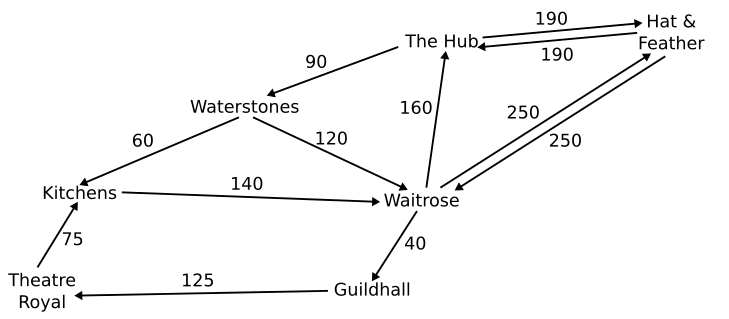
For example:

• $V$ = {1, 2, 3, 4, 5}
• $E$ = {(1, 2), (1, 3), (3, 5), (2, 5), (5, 4)}

Terminology §

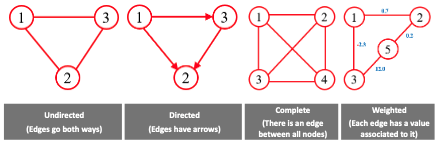
• An undirected graph has no arrows on edges.
• A directed graph or digraph has arrows on edges.
• Two nodes connected by an edge are adjacent.
• A weighted graph has values attached to edges.
• A path from a node back to itself is a cycle.
• An undirected graph with no cycles is a tree.
• A directed graph with no cycles is a directed acyclic graph or DAG.
• A DAG where no node is pointed to by more than one node is a directed tree.
• A complete graph is normally an undirected graph with an edge between each pair of vertices.

Graph Search §

We start at the source node and search until we find the target node. We normally want to visit each node once and only once.

• Depth-First Search
• Exhaustive Search
• Breath-First Search
• Best-First Search - A* Search
• Minimum Spanning Tree (MST) - Prim’s

Paths §

A sequence of k vertices, [v1, v2, ..., vk], such that any pair of consecutive vertices, vi, vi+1 are adjacent (connected by an edge) is called a path.

How do we represent a graph when it comes to implementation? §

We often represent a graph as a matrix (2D array), although other data structures can be used depending on the application.

If we have $N$ nodes to represent: for an $N$ by $N$ matrix $G$, a non-zero value of $g_{ij}$ ($i$th row, $j$th column of $G$) means there is an edge between node $i$ and $j$.

Undirected §

• We assume that $g_{ij}$ is the same as $g_{ji}$.

Directed §

• $g_{ij}$ is not always the same as $g_{ji}$.

Non-weighted §

• $g_{ij}$ is either one for an edge or zero for no edge.

Weighted §

• $g_{ij}$ is the edge weight or zero for no edge.

Complete §

• $g_{ij}$ is never zero.

Adjacency Matrix - Recap §

If we have $N$ nodes to represent:

• For an $N$ by $N$ matrix $G$ a non-zero value of $g_0$ ($i$th row $j$)

See also §

• Trees
• Dijkstra
• Floyd-Warshall
• Inkblot
• Graphviz