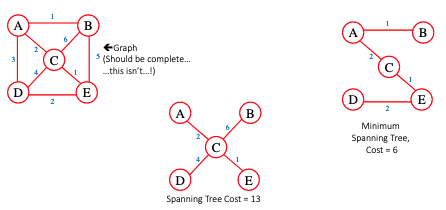
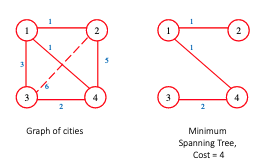
It is a subtree with the minimum possible edge weight that connects all nodes together.
There must exist no cycles in the tree, meaning it is usually a complete graph.
The cost of a spanning tree is the sum of all the edge weights and a minimum spanning tree (MST) is the spanning tree with the minimum cost.
A graph can have multiple minimum spanning subtrees:

The two most popular algorithms are Kruskal’s and Prim’s.
Example
Applications
Network Design:
- Computer networks, telecommunications networks, transportation networks, water supply networks etc.
CfA redshift survey:
- MSTs used for understanding the large-scale structure of the universe.
Approximation algorithms for NP-hard problems:
- Travelling salesperson problem.
Cancer imaging:
- The British Columbia Cancer Research centre uses them to describe the arrangements of nuclei in skin cells.
Visualisation
Prim’s Algorithm for working out the Minimum Spanning Trees: https://www.cs.usfca.edu/~galles/visualization/Prim.html