It is used to determine the shortest path from one node in the graph to every other node within the same graph, provided they can be reached from the source node.
Its complexity is .
The graph must have non-negative weights on all edges.
How It Works
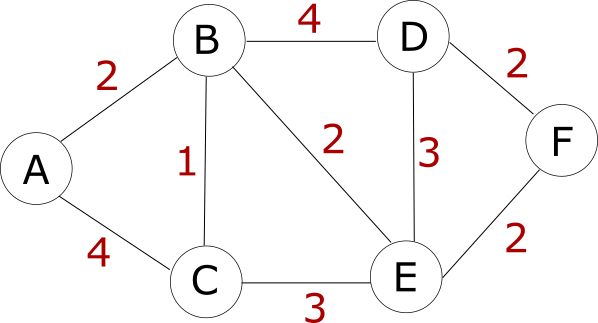
- Given the graph above, to find the shortest path between A and F, three values need to be initialised:
- Array of distances from the source node (A) to each node in the graph. The weight of the source node is instantiated as 0 while all the other nodes initial value is infinity.
- Array of all nodes in the graph, which will be empty by the end (unvisited array).
- Array of all the nodes that the algorithm has visited, which by the end will contain all the nodes of the graph (visited array).
Example
Starting from the source (A), we visit its neighbour with the lowest weight (B).
We then check:
if (D[current_node]) + D[adjacent_edge] < D[adjacent])If true, we update the adjacent distance with the new shortest path.
Using A as a starting point, from A to B: D = 0 + 2 which is < D[B] = infinity. Therefore, we update.
As you can see on the graph, when in current node A (starting node), the cost of going to its neighbours, B and C, is of 2 and 4 respectively. Because 2 and 4 are less than B and C current values (infinity), we update the table.
Note that the letter next to the number indicates what path is was taken:
| Current Node | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 0A | 2A | 4A |
Now with B being the current node, we repeat. For example, to get C there is a cost of 1. We sum B’s current distance from the source with the distance to C and check if it is less than the current value (infinity).
| Current Node | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 0A | 2A | 4A | |||
| B | 0A | 2A | 3B | 6B | 4B |
Now moving on to C, it has only one unchecked neighbour, E. The cost of getting to E, through C, is 4 + 3 = 7. However, the cost of getting to E (through B) is currently 4. Therefore, we don’t update the table as C isn’t the shorted path to E.
We then iterate until we visit all the nodes. The completed table for that graph would look like this:
| Current Node | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 0A | 2A | 4A | |||
| B | 0A | 2A | 3B | 6B | 4B | |
| C | 0A | 2A | 3B | 6B | 4B | |
| E | 0A | 2A | 3B | 6B | 4B | 6E |
| D | 0A | 2A | 3B | 6B | 4B | 6E |
| F | 0A | 2A | 3B | 6B | 4B | 6E |
See also
Failure
Error: There is another generation process
plugin:obsidian-textgenerator-plugin:56949 TextGenerator.eval plugin:obsidian-textgenerator-plugin:56949:31
Generator.next
plugin:obsidian-textgenerator-plugin:78 eval plugin:obsidian-textgenerator-plugin:78:61
new Promise
plugin:obsidian-textgenerator-plugin:62 __async plugin:obsidian-textgenerator-plugin:62:10
plugin:obsidian-textgenerator-plugin:56935 TextGenerator.generate plugin:obsidian-textgenerator-plugin:56935:12
plugin:obsidian-textgenerator-plugin:58440 AutoSuggest.eval plugin:obsidian-textgenerator-plugin:58440:52
Generator.next
plugin:obsidian-textgenerator-plugin:78 eval plugin:obsidian-textgenerator-plugin:78:61
new Promise