Floyd-Warshall §

---

It is a shortest path algorithm that calculates the shorted path between all pairs of vertices.

• Negative edges are allowed.
• No negative cycles.
• $O(V^3)$, where V is the number of vertices.

Pseudo-code §

let V = number of vertices of graph
let dist[V][V] = 2D array of minimum distances (the answers)
 
for each vertex v
  dist[V][V] <- 0
 
for each edge (u, v)
  dist[u][V] <- weight(u,V)
 
for k from 1 to V
  for i from 1 to V
    for j from 1 to V
      if dist[i][j] > dist [i][k] + dist[k][j]
       dist[i][j] <- dist[i][k] + dist[k][j]

Example §

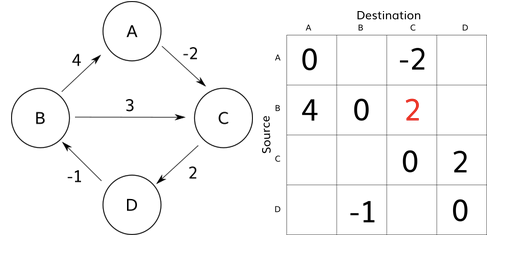
Here is a graph with four vertices (V = 4) and dist[4][4]:

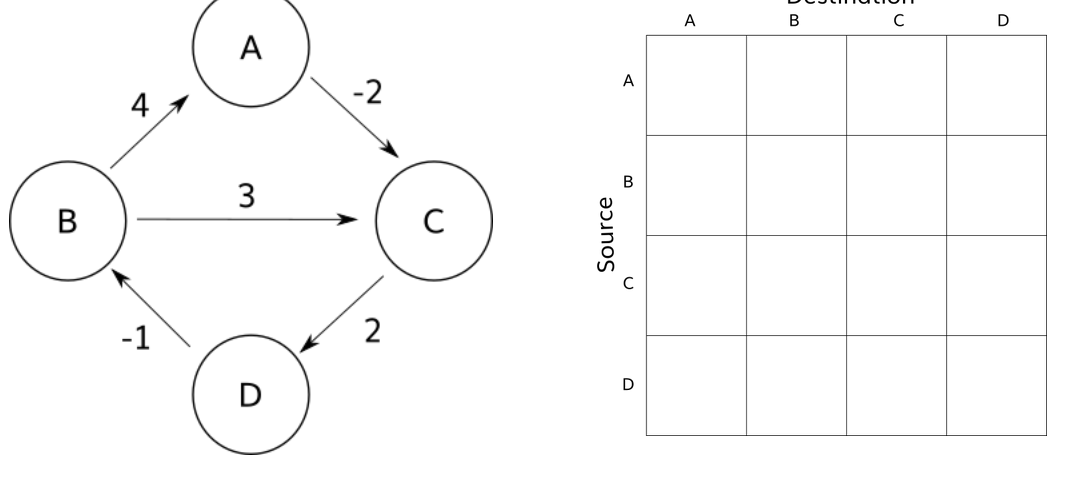
for each vertex v
  dist[v][v] <- 0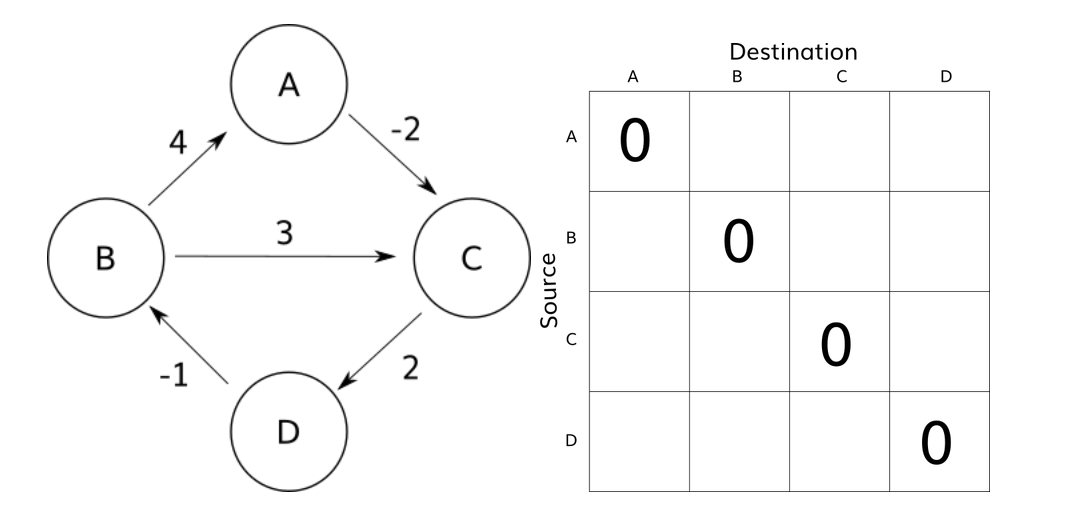

for each edge (u,v)
  dist[u][v] <- weight(u,v)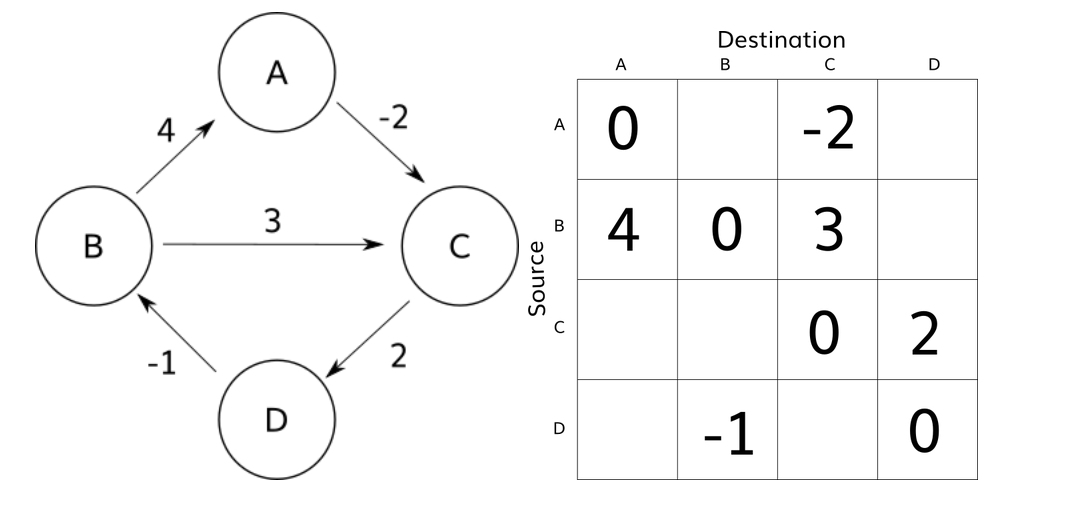

for k from 1 to V
  for i from 1 to V
    for j from 1 to V
    if dist[i][j] > dist[i][k] + dist[k][j]
      dist[i][j] <- dist[i][k] + dist[k][j]

If k = A, i = A and j = A:

dist[i][j] > dist[i][k] + dist[k][j]
dist[A][A] > dist[A][A] + dist[A][A]
    0      >     0      +     0

This statement is false. Therefore, dist does not get updated:

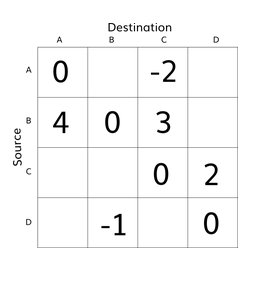
If k = A, i = A and j = B then there is not yet a value for A->B. It is assumed to be infinite:

dist[i][j] > dist[i][k] + dist[k][j]
dist[A][B] > dist[A][A] + dist[A][B]
 infinity  >     0      +  infinity

This statement is false. Therefore, dist does not get updated.

If k = A, i = B and j = C:

dist[i][j] > dist[i][k] + dist[k][j]
dist[B][C] > dist[B][A] + dist[A][C]
    3      >     4      +    -2

This statement is true. Therefore, dist gets updated:

See also §

• Dijkstra
• Graphs
• Big O Notation