Supervised Learning

---

Introduction §

• Classification attempts to solve the problem of assigning classes to data.
• It involves allocating a class to new, unassigned cases based on existing data.

Example:

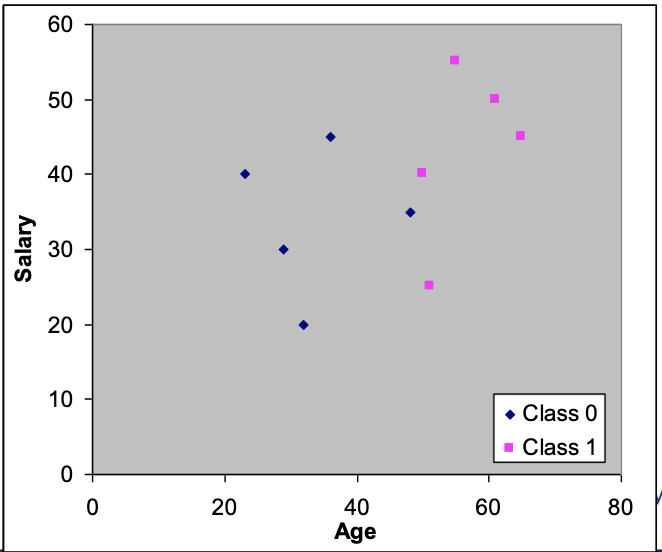
Case	Age	Salary	Class
1	50	40	1
2	32	20	0
3	36	45	0
4	55	55	1
5	61	50	0
6	29	30	0
7	48	35	0
8	65	45	1
9	23	40	0
10	51	25	1

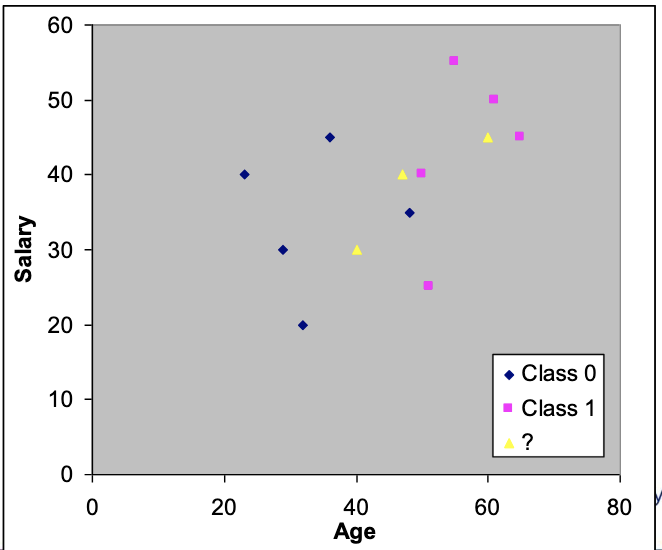
New data:

Case	Age	Salary	Class
11	60	45	?
12	40	30	?
13	47	40	?

---

cs3002-supervised-learning-decision-trees §

---

cs3002-supervised-learning-knearest-neighbour §

---

Testing Performance §

• Aim is to classify new unseen data.
• Often look at a simple error rate to assess our classifiers.
• error = number of errors / number of cases
• Empirical error rate is not the same as true error rate.
  • Empirical is based on a sample.
  • True is based on infinite cases.
• Is it possible to estimate the true error rate?

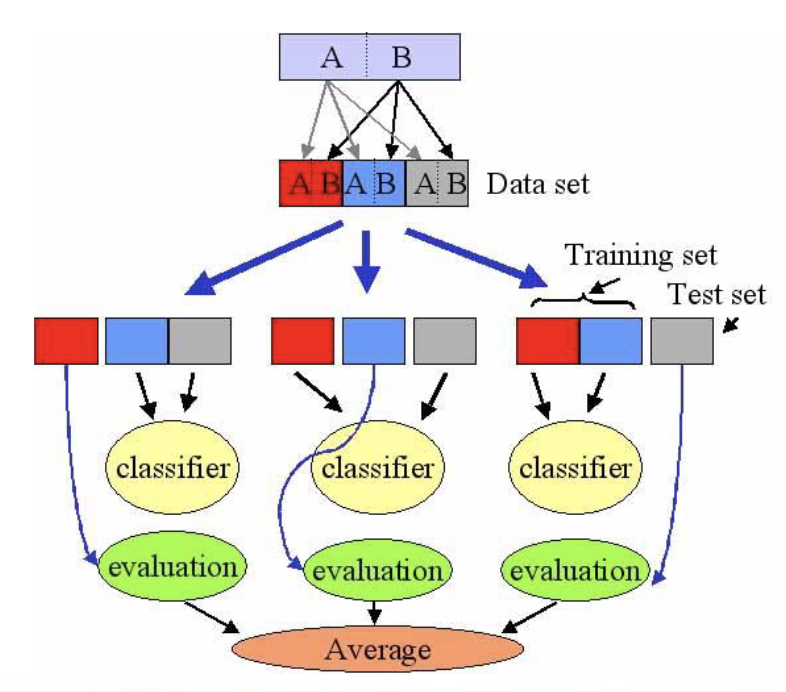
Training and Test Sets §

• Obviously a good idea to split data into a training set and a test set.
• Known as the holdout method.
• Use training set to learn model.
• Use test set to score the accuracy.
• Ideally the two sets are independent (generated separately).

Resampling §

• What if the sample of data is small or biased?
• Resampling methods can be used.
  • Randomly select training and test sets.
  • Repeat for a fixed number of iterations.
• Methods include:
  • Cross-validation.
  • Bootstrapping.

Cross-validation §

• K-fold cross validation:
  • Randomly split the data up into $k$ subsets of equal size.
  • Remove one of the subsets and train classifier on remaining subsets.
  • Test on the removed subset.
  • Repeat for all subsets.
• Cross-validation is considered an unbiased estimator of true error.

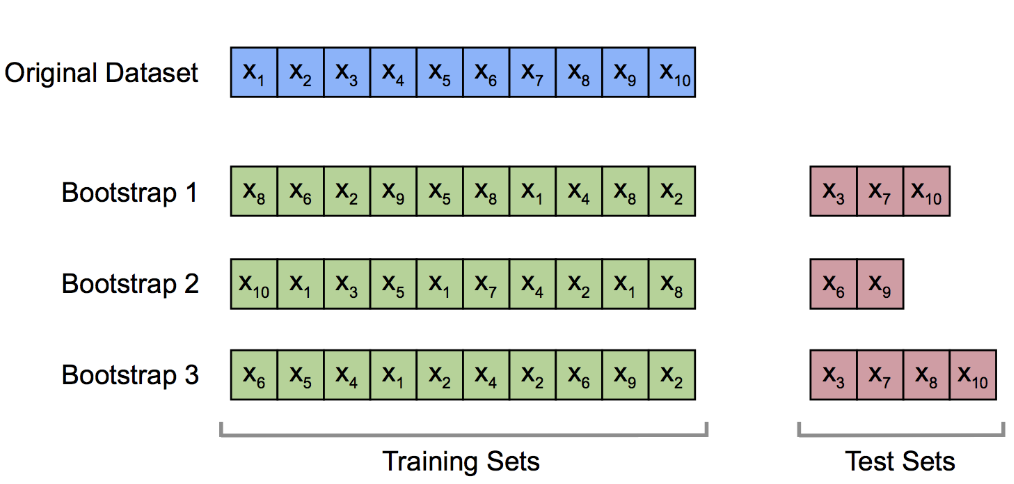
Bootstrapping §

• For the bootstrap $n$ training data items are sampled with replacement from $n$ cases.
• Cases that are not found in the training set are used for the test set.
• Generally produces worse rates than the true error rate (worse case scenario).

Resampling and Random Forests §

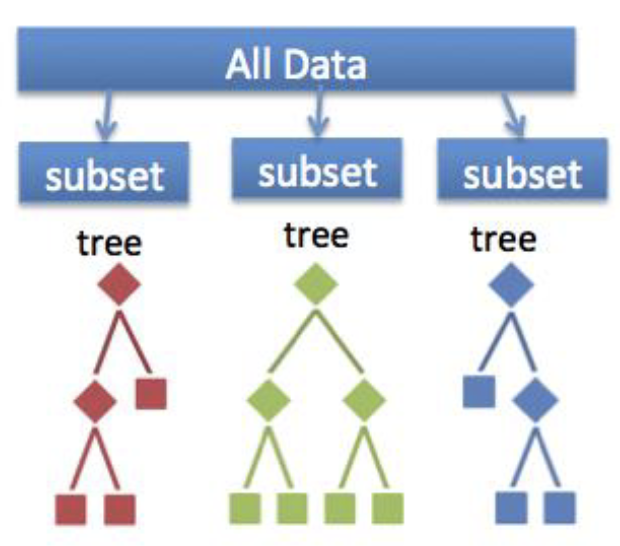
cs3002-supervised-learning-confusion-matrix §

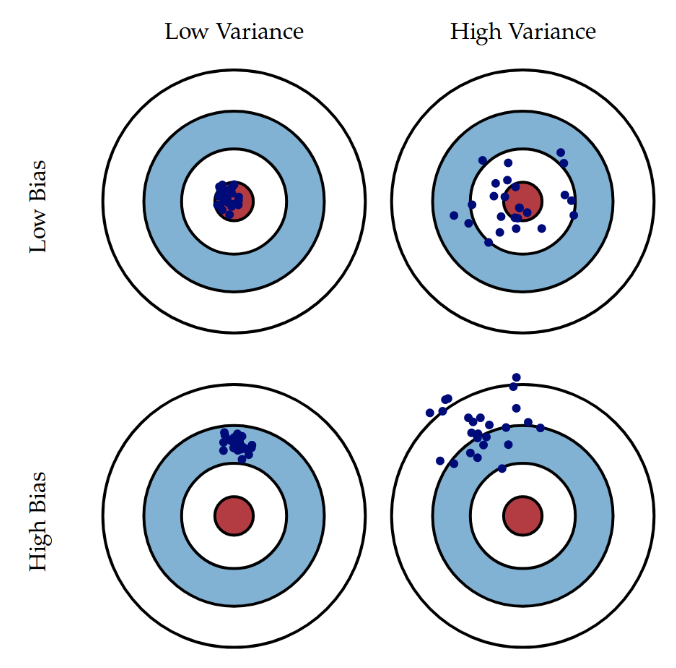
Bias, Variance and Overfitting §

• Consider two models:

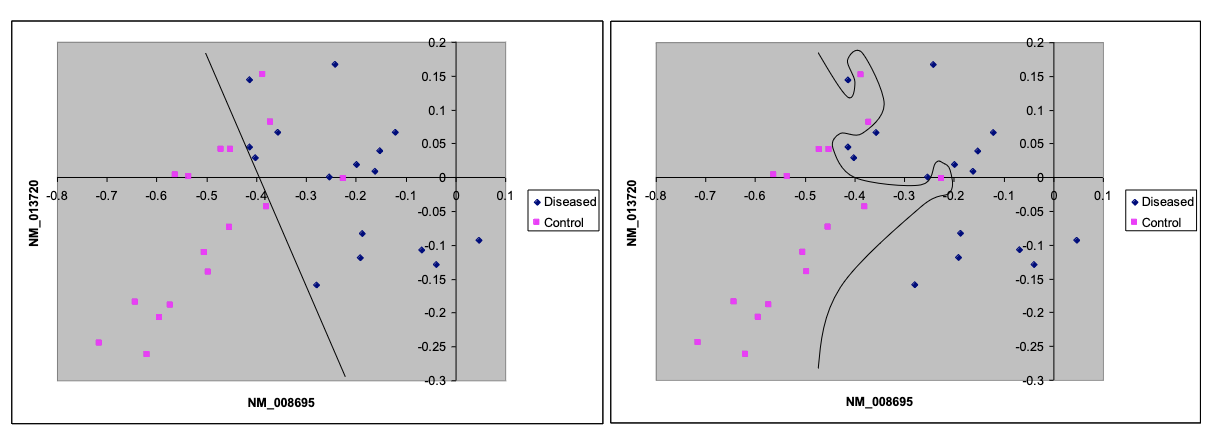
• Bias is some systematic error in the model.
• Variance is the difference from one model to the next.
• The first model (straight line) has high bias.
• The second has high variance:
  • It fits the data very well.
  • But it will not predict new cases.
  • It has overfit to the data.

Summary §

• Decision Trees
  • Decision trees use a tree-like structure to make decisions and classify data.
  • They are easy to interpret but can be prone to overfitting, although pruning can help mitigate this.
• K-Nearest Neighbour
  • KNN is based on the proximity of data points in the feature space.
  • It’s easy to interpret, but it does not model data explicitly.
• Testing Performance
  • Different methods are used to assess classifier performance, such as sensitivity analysis.
• Resampling
  • Resampling techniques like cross-validation and bootstrapping are employed to address issues like small or biased datasets.
• Confusion Matrix, Sensitivity and Specificity
  • The confusion matrix is useful for considering the importance of errors.
  • Sensitivity and specificity are common measures for evaluating classifier performance.
• confuPrecision and Recall
  • Precision and recall are particularly relevant for imbalanced data, where one class is much larger than the other.
• ROC Curves vs. PR Curves
  • ROC curves illustrate the tradeoff between sensitivity and specificity.
  • PR curves illustrate the tradeoff between precision and recall.
• Bias, Variance, and Overfitting
  • Models can exhibit bias (systematic errors) or high variance (overfitting).
  • Overfit models may perform well on training data but poorly on new data.