cs3002-supervised-learning-confusion-matrix

• If errors are of differing importance:
  • E.g. failing to diagnose a disease can be more serious than diagnosing one that is not present.
• Then use a confusion matrix:
  • Class versus Prediction.
  • False positives and negatives.

Sensitivity and Specificity §

Common measures make use of false positives and negatives:

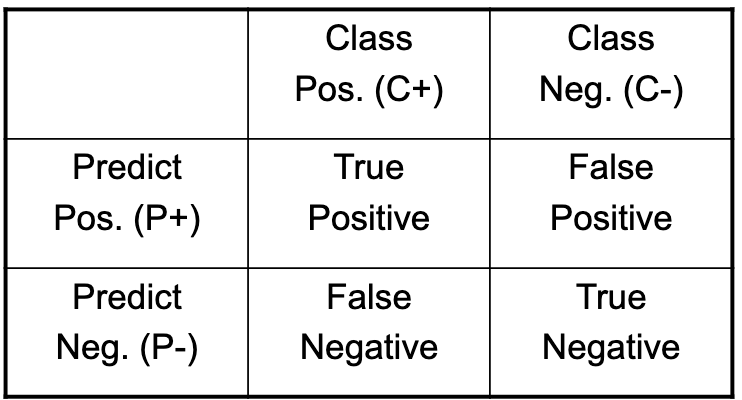
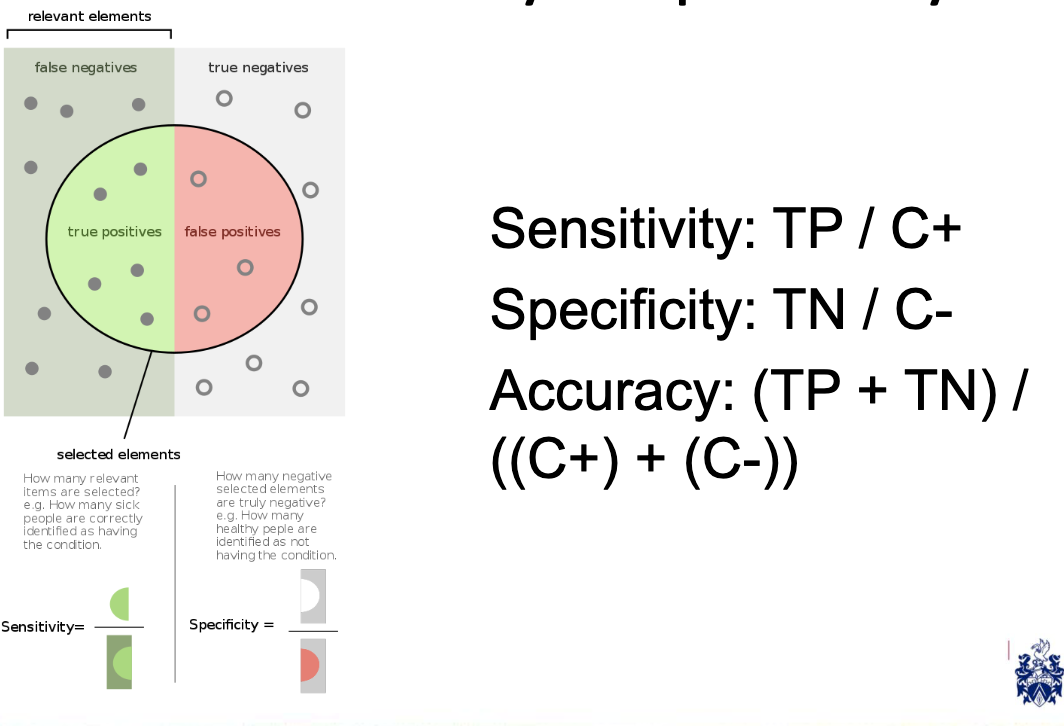
• For example, a classifier can have high sensitivity if it successfully classifies people who have developed cancer but a low specificity if it also classifies non-sufferers with cancer.

• But what about data where there are only a few positive cases: imbalanced?

Examples:

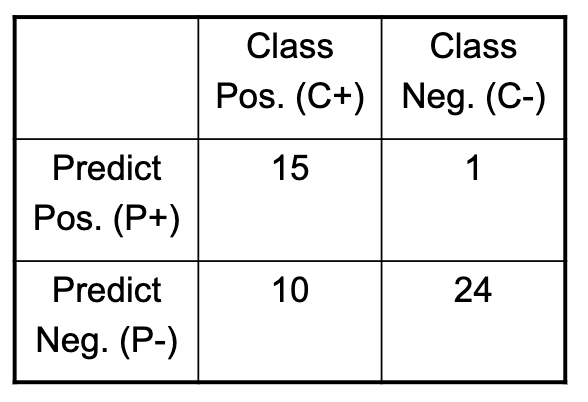
	Class Pos. (C+)	Class Neg. (C-)
Predict Pos. (P+)	15	1
Predict Neg. (P-)	10	24

• True Positives (TP) = 15
• False Positives (FP) = 10
• True Negatives (TN) = 24
• False Negatives (FN) = 1

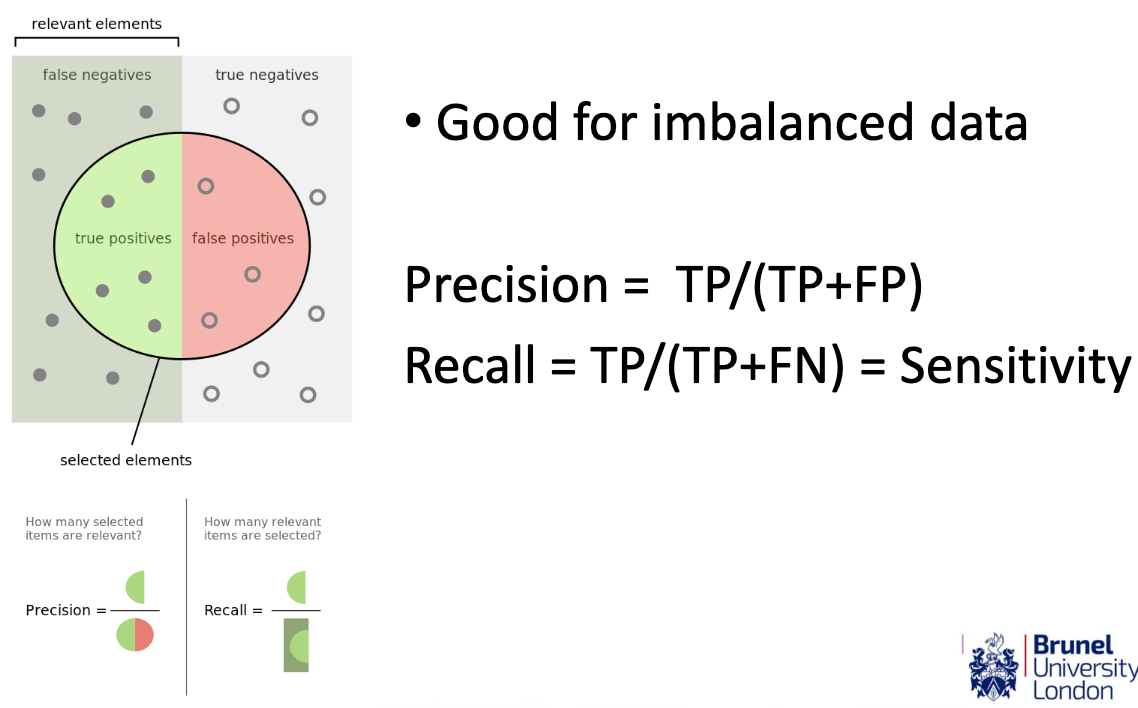
Precision (P) is defined as TP / (TP + FP), and Recall (R) is defined as TP / (TP + FN). The F1-score is the harmonic mean of precision and recall, given by:

$F1=2\ast (P\ast R)/(P+R)$

In this case, for Confusion Matrix 1:

• Precision (P) = 15 / (15 + 10) = 15 / 25 = 0.6
• Recall (R) = 15 / (15 + 1) = 15 / 16 ≈ 0.9375

$F1=2\ast (0.6\ast 0.9375)/(0.6+0.9375)\approx 0.7308$

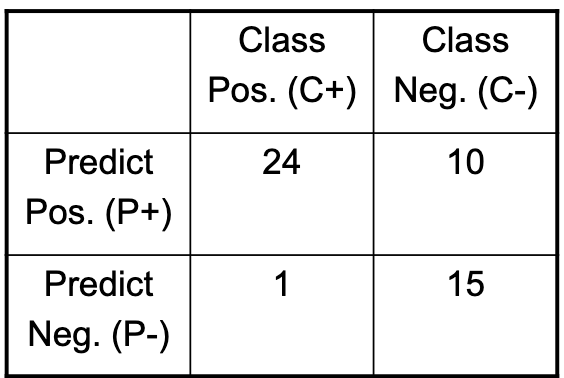
	Class Pos. (C+)	Class Neg. (C-)
Predict Pos. (P+)	24	10
Predict Neg. (P-)	1	15

• True Positives (TP) = 24
• False Positives (FP) = 1
• True Negatives (TN) = 15
• False Negatives (FN) = 10

For Confusion Matrix 2:

• Precision (P) = 24 / (24 + 1) ≈ 0.960
• Recall (R) = 24 / (24 + 10) = 24 / 34 ≈ 0.7059

$F1=2\ast (0.960\ast 0.7059)/(0.960+0.7059)\approx 0.8149$

---

• Which would be most suitable for detecting patients with high-risk of cancer for follow up tests?

Comparing the F1-scores:

• F1-score for Confusion Matrix 1 ≈ 0.7308
• F1-score for Confusion Matrix 2 ≈ 0.8149

Based on the F1-scores, Confusion Matrix 2 is more suitable for detecting patients with a high risk of cancer for follow-up tests. It has a higher F1-score, indicating a better balance between precision and recall. This means that Matrix 2 has a higher likelihood of correctly identifying high-risk patients while keeping false positives relatively low.

---

• Which would be best for selecting patients for high-risk surgery?

When selecting patients for high-risk surgery, you typically want to prioritize patient safety and ensure that those chosen for the surgery have a low risk of complications. In this case, you should consider high precision as a priority because you want to minimize the number of false positives (i.e., patients who are not suitable for high-risk surgery but are selected).

Precision is defined as the ratio of true positives to the total number of predicted positives, and it measures the accuracy of positive predictions. In the context of selecting patients for high-risk surgery, high precision means that a high proportion of the selected patients are indeed suitable for the surgery, reducing the risk of operating on patients who may not benefit from it.

Let’s calculate the precision for both confusion matrices:

Confusion Matrix 1:

• True Positives (TP) = 15
• False Positives (FP) = 10

Precision (P) is defined as TP / (TP + FP), and for Confusion Matrix 1:

$P=15/(15+10)=15/25=0.6$

Confusion Matrix 2:

• True Positives (TP) = 24
• False Positives (FP) = 1

For Confusion Matrix 2:

$P=24/(24+1)\approx 0.960$

Comparing the precisions:

• Precision for Confusion Matrix 1 = 0.6
• Precision for Confusion Matrix 2 ≈ 0.960

Based on the precision values, Confusion Matrix 2 is more suitable for selecting patients for high-risk surgery. It has a significantly higher precision, meaning that a higher proportion of selected patients are likely suitable for the surgery, reducing the chances of unnecessary high-risk procedures on unsuitable candidates.

---

• Which is the best?

In general, the choice between the two confusion matrices depends on your specific objectives and priorities. There isn’t a one-size-fits-all answer as to which is “best” because it depends on the trade-offs between precision and recall, and your priorities may vary based on the application.

• Confusion Matrix 1 (lower precision, higher recall) is more suitable if you want to cast a wider net and prioritise capturing as many true positives as possible, even if it means accepting a higher risk of false positives. This approach is more lenient in selecting patients, which can be beneficial if you want to ensure that you don’t miss any patients who may genuinely benefit from high-risk surgery.

• Confusion Matrix 2 (higher precision, lower recall) is more suitable if you prioritise patient safety and want to minimise the chances of conducting high-risk surgery on patients who are not suitable. It provides a higher degree of certainty that selected patients are indeed appropriate candidates for high-risk surgery, even if it means potentially missing some who are suitable (lower recall).

In many real-world medical applications, patient safety and minimising unnecessary procedures are of paramount importance. Therefore, Confusion Matrix 2 (higher precision) is often preferred, as it minimises the risk of false positives and the associated risks and costs. However, the specific context, risks, and objectives of the high-risk surgery scenario may influence the choice between these two matrices.

Precision and Recall §

Good for imbalanced data:

ROC Curves vs PR Curves §

• Receiver Operating Characteristic curve:
  • Sensitivity / Specificity tradeoff.

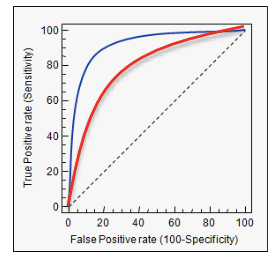
• Precision Recall curve:
  • Precision / Recall tradeoff.