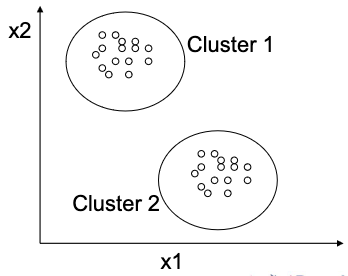
Clustering

Partition dataset into subsets (clusters), so that the data in each subset shares some common trait, often similarity or proximity.

Clusters are collections of similar objects without the need for ‘teacher’ signals.

A collection of objects which are “similar” between them and are “dissimilar” to the objects belonging to other clusters.

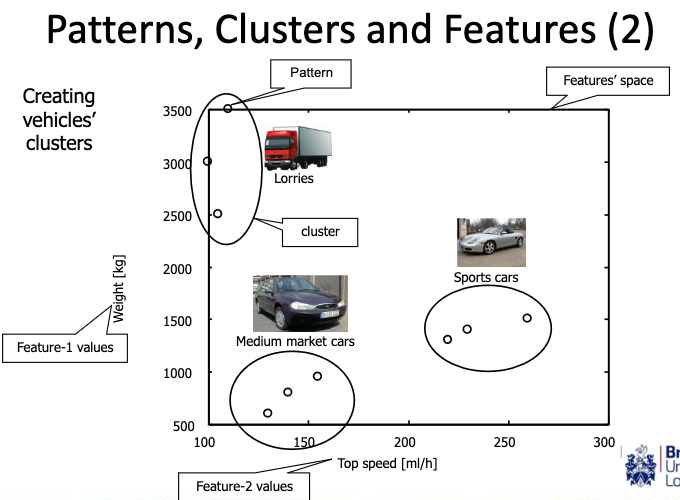
Applications of Clustering

For purposes like marketing, terror networks, resource allocation in companies/universities.

Customer Segmentation

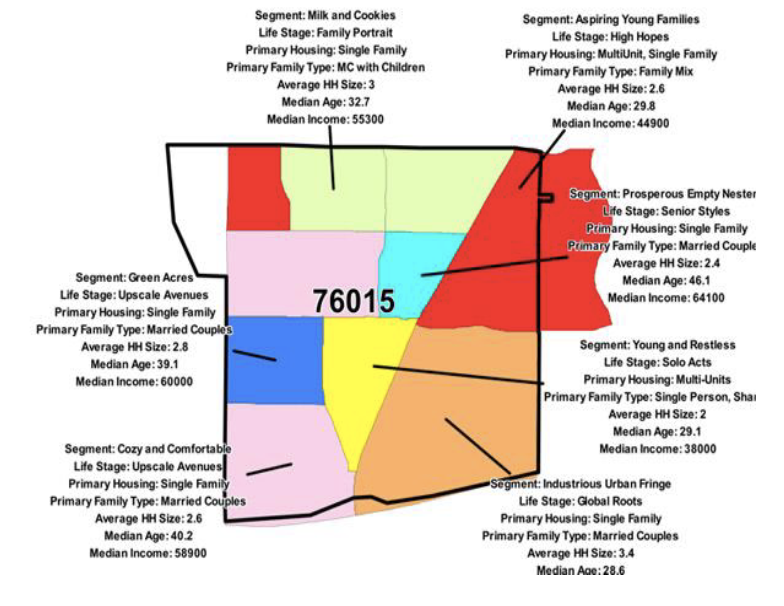
Gene Networks

Helps understand gene interactions and identify genes linked to diseases.

Methodologies for Clustering

How to do Clustering?

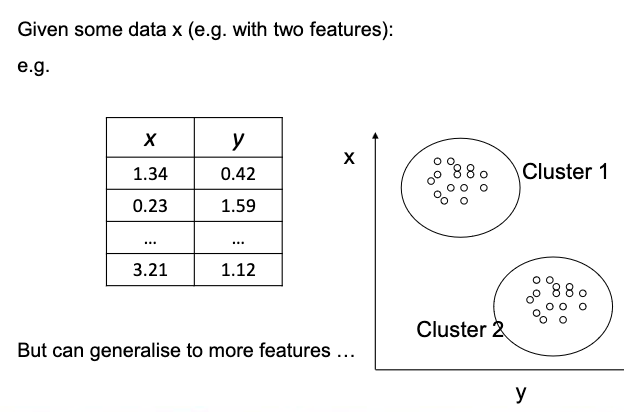
Pattern Similarity and Distance Metrics

Clusters are formed by similar patterns.
Commonly adopted similarity metric is distance.
Euclidean and Manhattan distances are commonly used metrics.

More distance metrics:

Correlation.
Minkowski.
Mahalanobis.

They are often application dependant. The important things are the shape, distance and scale.

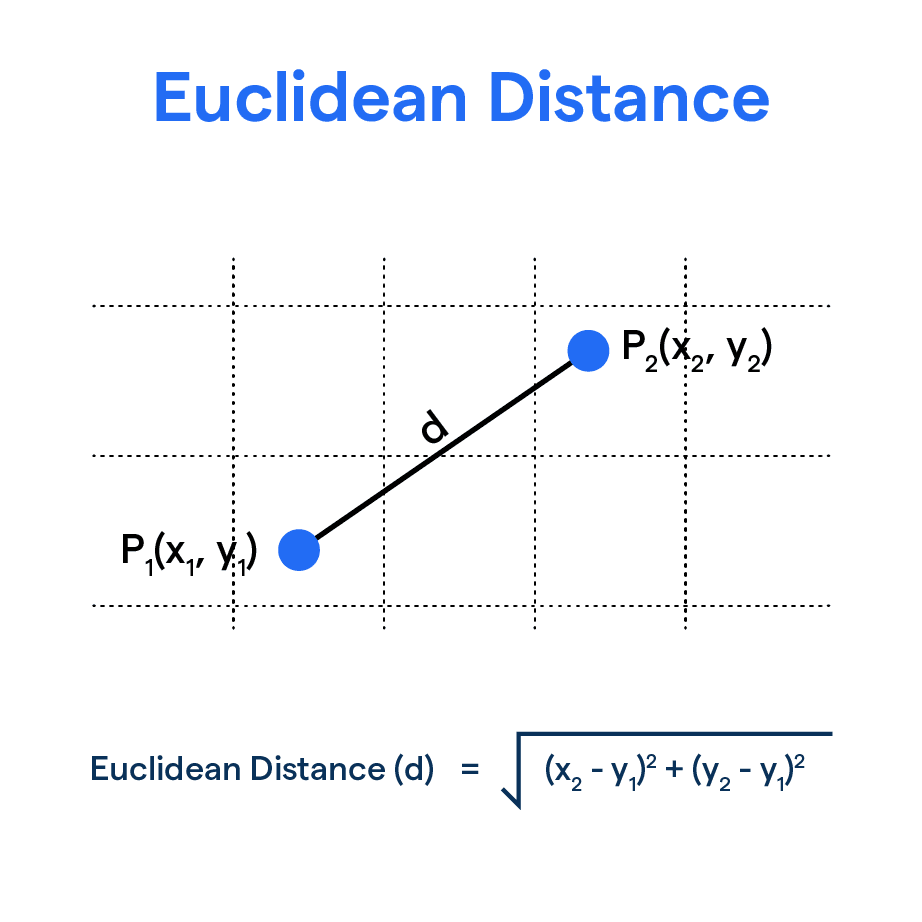
Euclidean

The square root of the sum of the squared differences between coordinates.

Formula: $(d (x, y) = (x_{1} - y_{1})^{2} + (x_{2} - y_{2})^{2} + \dots + (x_{N} - y_{N})^{2})$

Example

x	5.5	2.9	4.8	6.7	0.6
y	0.2	1.0	4.8	3.8	9.2

Therefore, $d (x, y)$ :

$= ((5.5 - 0.2)^{2} + (2.9 - 1.0)^{2} + (4.8 - 4.8)^{2} + (6.7 - 3.8)^{2} (0.6 - 9.2)^{2})$

$= ((5.3)^{2} + (1.9)^{2} + (0.0)^{2} + (2.9)^{2} + (- 8.6)^{2})$

$= (28.09 + 3.61 + 0.0 + 8.41 + 73.96)$

$= (114.07) = 10.68$

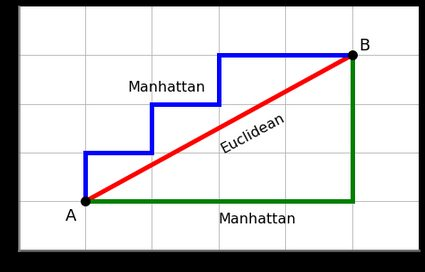
Manhattan

The sum of the absolute differences between the coordinates of two points.

Formula: $(d (x, y) = ∣ x_{1} - y_{1} ∣ + ∣ x_{2} - y_{2} ∣ + \dots + ∣ x_{N} - y_{N} ∣)$

Therefore, $d (x, y)$ :

$(∣5.5 - 0.2∣ + ∣2.9 - 1.0∣ + ∣4.8 - 4.8∣ + ∣6.7 - 3.8∣ + ∣0.6 - 9.2∣)$

$= 5.3 + 1.9 + 0.0 + 2.9 + 8.6$

$= 18.7$

Embeddings

It means to map data onto a new space to capture different characteristics.

The distance between points has some meaning.

K-Means Clustering

Hierarchical Clustering

Limitations of K-Means and Hierarchical Clustering

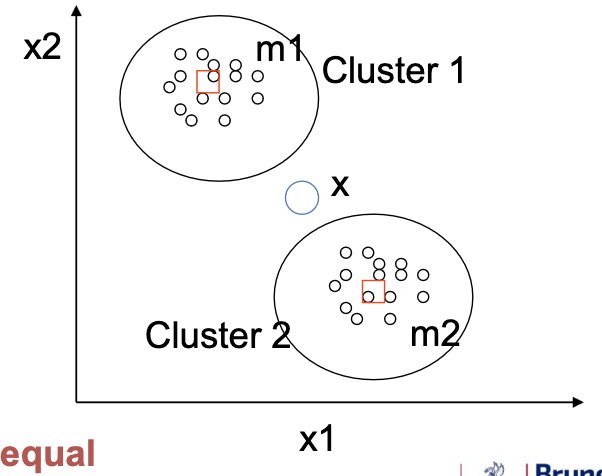
Challenges with Hard Assignment in Clustering

At each iteration, a pattern can be assigned to one cluster only (the assignment is hard).

For example, x here in the middle of the two cluster centroids will either:

drag m1 down, or
drag m2 up.

Other Clustering Methods

Fuzzy Clustering

For example: Fuzzy c-Means.

No sharp boundary.
Fuzzy clustering is often better suited.
Fuzzy c-Means is a fuzzification of k-Means and the most well-known.

The cluster membership is now a weight between 0 or 1 and the distance to a centroid is multiplied by the membership weight.

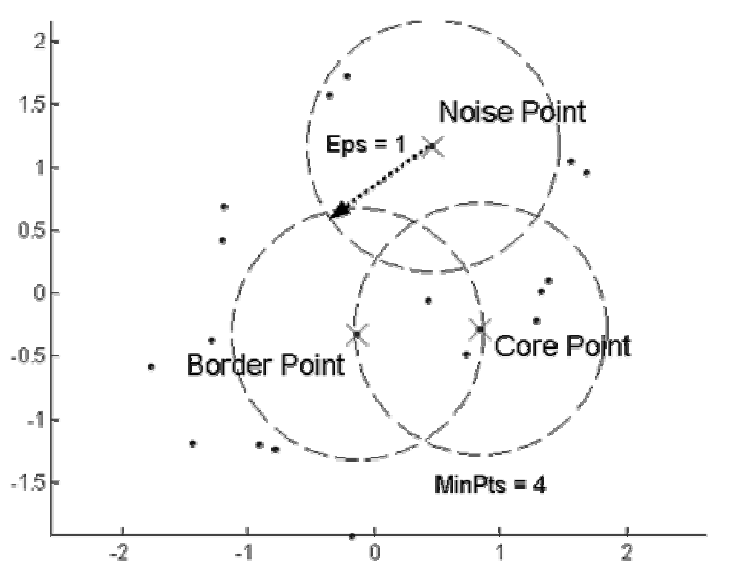
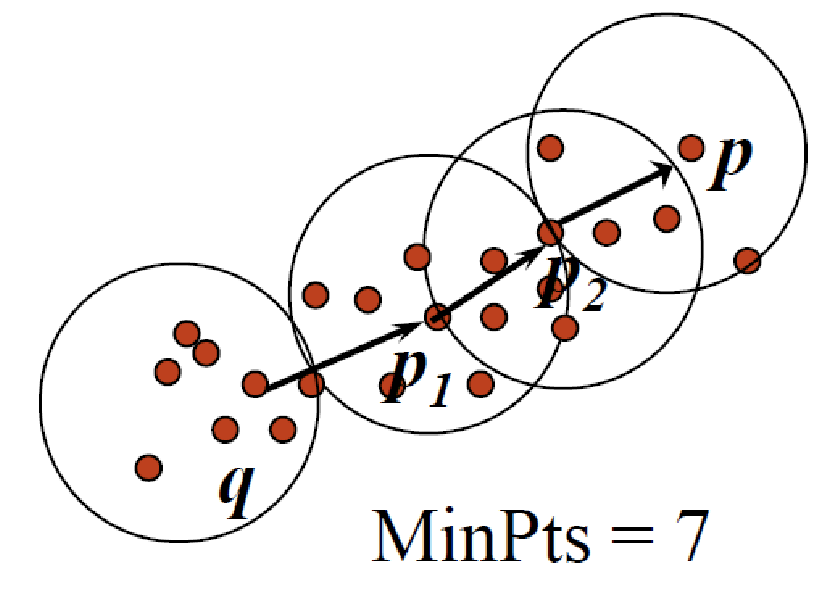
DBSCAN

Density based clustering algorithm, density being the number of points within a specified radius (Eps).
A point is a core point if it has more than a specified number of points (MinPts) within Eps.
Core point is in the interior of a cluster.

Evaluating Cluster Quality

How do we know if the discovered clusters are any good?

The choice of metric is vital.

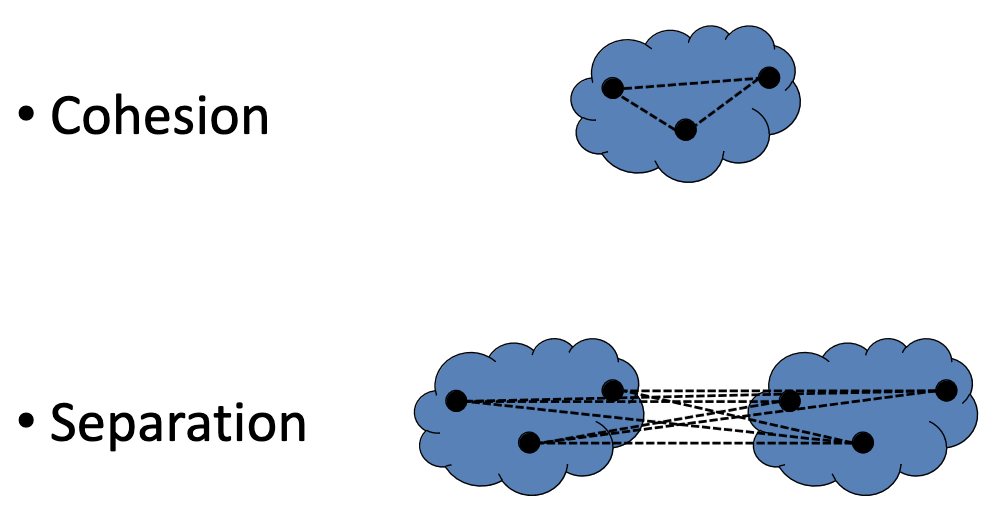
Cohesion and Separation

Reduce separation and increase cohesion.

Supervised

We can use the “true clusters” to test the effectiveness of different clustering algorithms.

Comparing Clusters

We can use metrics to measure how similar two arrangements are.

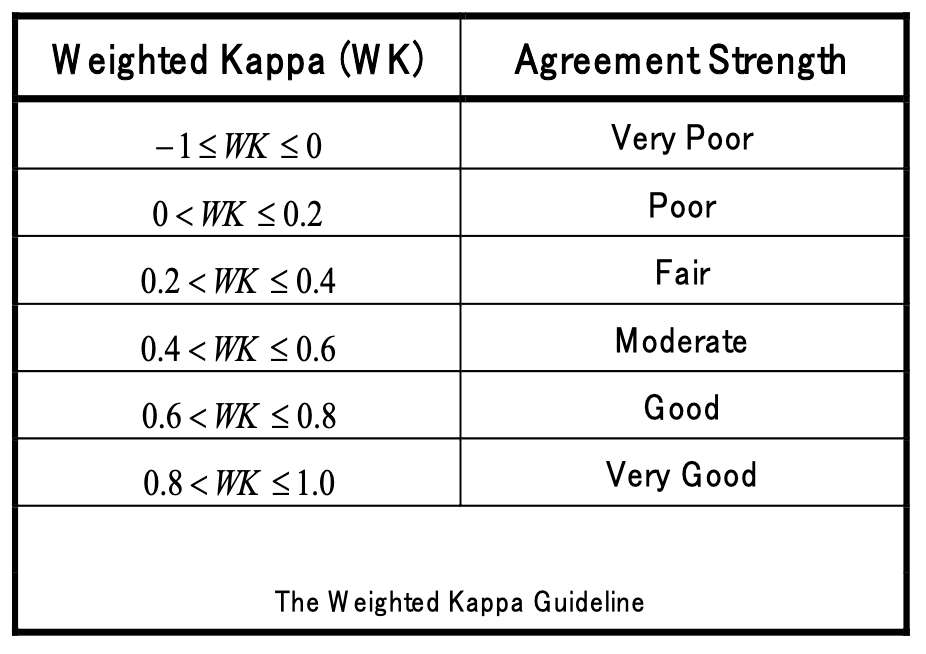
Weighted-Kappa

0 is random.
-1 something weird is going on.
Between 0.8 and 1 is good.

Association Rules

Reading

Principles of Data Mining Chap 9 Section 9.3
Pang-Ning Tan “Introduction to Data Mining” (Chapter 8): http://www-users.cs.umn.edu/~kumar/dmbook/index.php
Anil Jain: “Data Clustering: 50 Years Beyond K-Means”, Pattern Recognition Letters
Tang et al., Kumar, Introduction to Data Mining (Chapter 6): https://www-users.cs.umn.edu/~kumar001/dmbook/index.php

✨ Morioh