- Running time.
- Pseudo-code.
- Counting primitive operations.
Running Time
Varies with the input and typically grows with the input size.
An algorithm may run faster on certain data set compared to others.
We have the following run times:
- Best case.
- Not very informative as it might not happen very often.
- Worst case.
- Easier to analyse, crucial to applications such as traffic control etc.
- Average case.
- Take all inputs, calculate time for all inputs then sum all calculated values and divide by total inputs.
We can use System.currentTimeMillis() for example to get a measure of running time in Java.
Limitations
- We would need same software and hardware environments.
- Sometimes difficult to implement algorithm.
- One algorithm can perform better than the rest for some inputs.
The solution is asymptotic analysis.
Asymptotic Analysis
It uses a high-level description of the algorithm instead of an implementation.
We evaluate the performance of an algorithm in terms of input size and calculate how does the time taken by an algorithm increases with the input size.
T(n)
We use it to measure the running time/computation of an algorithm.
Where n is the size of the input, if there is more than one input we might have T(n,m) where n and m are the sizes of the inputs.
We can use T(n) to calculate the Big O.
Pseudo-Code
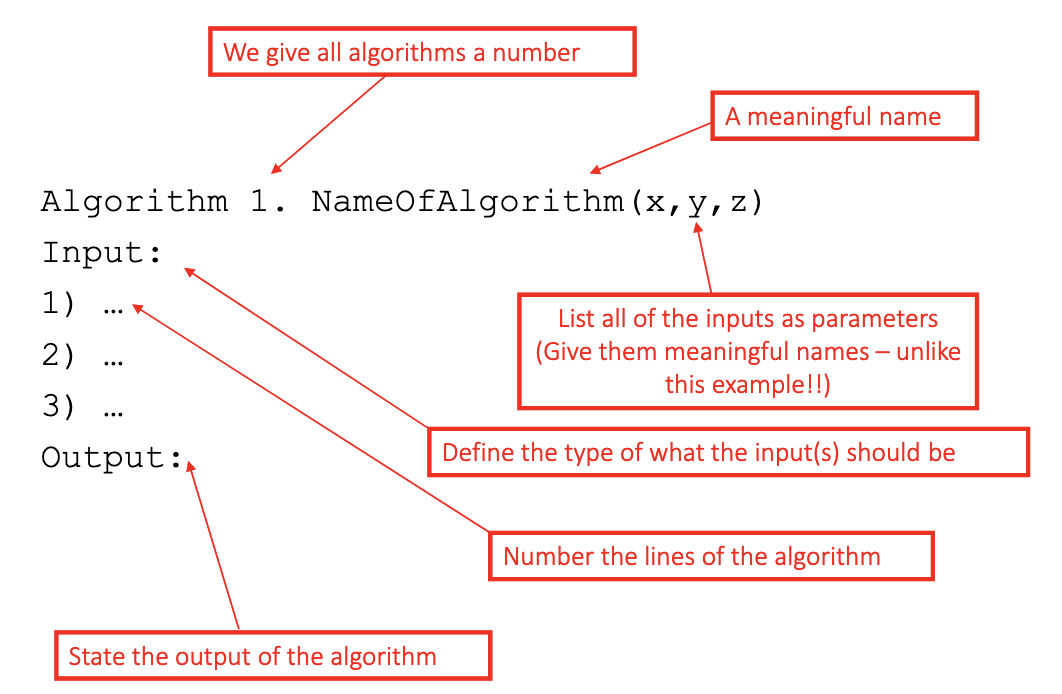
We do not call functions unless we describe the pseudo-code for them or describe what they do.
For example, we would not say:
X = Y.toLowerCase();
However we could say:
Let X equal the lower case version of Y
Variables

If Statements

For Loops

Full Example

Primitive Operations
They are basic computations performed by an algorithm, for example:
- Evaluating an expression (x>y)
- Assigning a value to a variable.
- Indexing into an array.
- Calling a method.
- Returning from a method.

The most difficult part is getting all of the nest loops correct.



- Normally if statements have 9 primitive operations.
