It picks a midpoint (approximate the median) and partition values, into those less than the midpoint (left) and greater (right).
Then recurse on each partition in turn until there is one value in each partition.
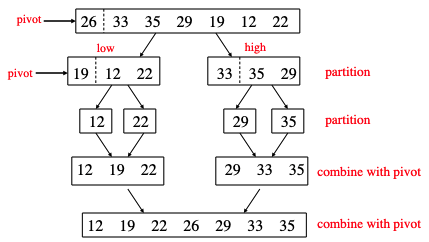
There are many different versions of Quicksort, based on the different ways of picking the pivot:
- Pivot always being the first element.
- Pivot always being the last element.
- Pivot is selected randomly.
- The median is chosen as the pivot.
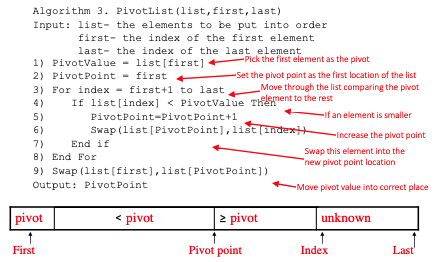
Pseudo-Code

PivotList Pseudo-Code
In the worst case, it will do comparisons, but creates one partition that has elements and the other will have no elements. This happens because we wind up reducing the partition by one element each time.
Worst case:
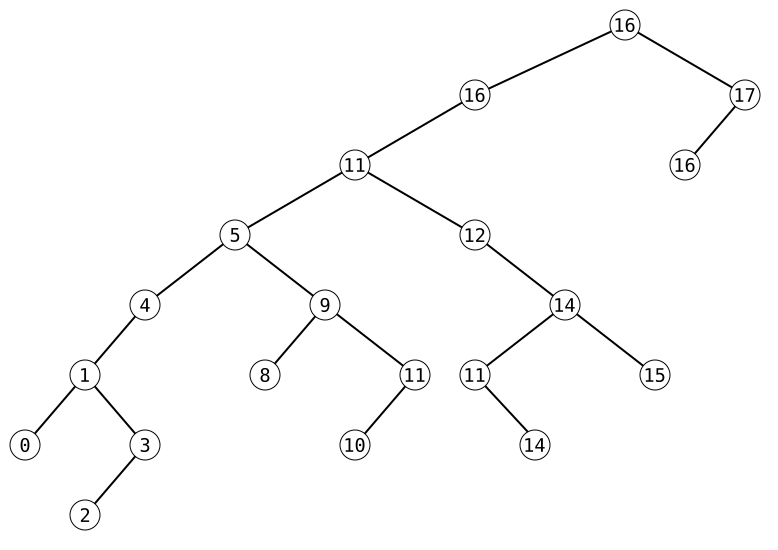
For the best case, it creates two parts that are the same size. Then all the subsequent parts are the same size as the algorithm calls itself, which can be modelled as a binary tree.
Best case:
Implementation
void
quicksort (int *a, int lo, int hi)
{
if (lo < hi)
{
int p = partition (a, lo, hi);
quicksort (a, lo, p);
quicksort (a, p + 1, hi);
}
}Issues
Note that this is big O notation.
Quicksort is critically dependant on choice of median. Taking best of low, high and mid points deals with the obvious case of sorted data.
It is implemented as qsort in the standard C maths library.
Quicksort Partition
int
partition (int *a, int lo, int hi)
{
int pivot = a[lo]; /* Guess median */
int i = lo - 1, j = hi + 1;
while (1)
{
do /* Leftmost element >= pivot */
i++;
while (a[i] < pivot);
do /* Rightmost element <= pivot */
j--;
while(a[j] > pivot);
if (i >= j)
return j;
swap (&(a[i]), &(a[j]));
}
}Output
16 16 0 14 9 11 10 2 3 4 1 11 8 17 14 5 11 12 15 16
16 16 0 14 9 11 10 2 3 4 1 11 8 17 14 5 11 12 15 16
16 15 0 14 9 11 10 2 3 4 1 11 8 17 14 5 11 12 16 16
16 15 0 14 9 11 10 2 3 4 1 11 8 12 14 5 11 17 16 16
11 15 0 14 9 11 10 2 3 4 1 11 8 12 14 5 16 17 16 16
5 15 0 14 9 11 10 2 3 4 1 11 8 12 14 11 16 17 16 16
5 8 0 14 9 11 10 2 3 4 1 11 15 12 14 11 16 17 16 16
5 8 0 11 9 11 10 2 3 4 1 14 15 12 14 11 16 17 16 16
5 8 0 11 9 1 10 2 3 4 11 14 15 12 14 11 16 17 16 16
4 8 0 11 9 1 10 2 3 5 11 14 15 12 14 11 16 17 16 16
4 3 0 11 9 1 10 2 8 5 11 14 15 12 14 11 16 17 16 16
4 3 0 2 9 1 10 11 8 5 11 14 15 12 14 11 16 17 16 16
4 3 0 2 1 9 10 11 8 5 11 14 15 12 14 11 16 17 16 16
1 3 0 2 4 9 10 11 8 5 11 14 15 12 14 11 16 17 16 16
0 3 1 2 4 9 10 11 8 5 11 14 15 12 14 11 16 17 16 16
0 2 1 3 4 9 10 11 8 5 11 14 15 12 14 11 16 17 16 16
0 1 2 3 4 9 10 11 8 5 11 14 15 12 14 11 16 17 16 16
0 1 2 3 4 5 10 11 8 9 11 14 15 12 14 11 16 17 16 16
0 1 2 3 4 5 8 11 10 9 11 14 15 12 14 11 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 14 15 12 14 11 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 14 15 12 14 11 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 11 15 12 14 14 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 11 14 12 15 14 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 11 12 14 15 14 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 11 12 14 14 15 16 17 16 16
0 1 2 3 4 5 8 9 10 11 11 11 12 14 14 15 16 16 16 17
0 1 2 3 4 5 8 9 10 11 11 11 12 14 14 15 16 16 16 17As a tree-sort
Code Example
/* Basic Quicksort
Copyright (C) 2020 Embecosm Limited <www.embecosm.com>
Contributor: Jeremy Bennett <jeremy.bennett@embecosm.com>
SPDX-License-Identifier: GPL-3.0-or-later */
/* This version uses Tony Hoare's original algorithm as described in Comp. J,
* 5(1), April 1962, pp 10-15. */
#include <stdlib.h>
#include <stdio.h>
#ifndef N
#define N 20
#endif
void
populate (int arr[])
{
for (int i = 0; i < N; i++)
arr[i] = rand () % N;
}
void
swap (int *a, int *b)
{
int t = *a;
*a = *b;
*b = t;
}
void
dump_array (int arr[])
{
for (int i = 0; i < N; i++)
printf ("%2d ", arr[i]);
printf ("\n");
}
int median (int x, int y, int z)
{
int b[] = {x, y, z};
int j, k;
for (k = 1; k < 3; k++)
for (j = k; (j > 0) && (b[j] < b[j - 1]); j--)
swap (&(b[j]), &(b[j - 1]));
return b[1];
}
/* Partition data around pivot, returning the index of the pivot as result */
int
partition (int *a, int lo, int hi)
{
#ifdef MEDIAN
int pivot = median (a[lo], a[hi], a[(lo + hi) / 2]);
#else
int pivot = a[lo];
#endif
int i = lo - 1; /* Don't worry gets incremented before use! */
int j = hi + 1; /* Don't worry gets decremented before use! */
while (1)
{
do /* Leftmost element >= pivot */
i++;
while (a[i] < pivot);
do /* Rightmost element <= pivot */
j--;
while (a[j] > pivot);
if (i >= j) /* Two pointers have met */
return j;
swap (&(a[i]), &(a[j]));
dump_array (a);
}
}
/* Find a pivot, partition around that pivot, recurse on each partition */
void
quicksort (int *a, int lo, int hi)
{
if (lo < hi)
{
int p = partition (a, lo, hi);
quicksort (a, lo, p);
quicksort (a, p + 1, hi);
}
}
int
main ()
{
int a[N];
int i, j, k, m;
srand (561U);
populate (a);
dump_array (a);
quicksort (a, 0, N - 1);
return 0;
}
/*
Local Variables:
mode: C
c-file-style: "gnu"
End:
*/