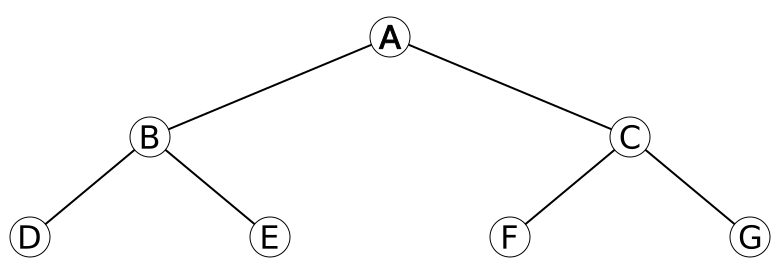
Binary Trees §

---

A binary tree is a set of nodes linked into a simple structure. Every node has at most two children.

• Each node has data, a left pointer and a right pointer.
• Each pointer can point to one other node (or be NULL).

Nomenclature §

• A node is the parent of any node to which it pointer.
• A node is the child of any node that points to it.
• A node can be a child and a parent.
• A node is the root of the tree if it has no parent.
• A node is a leaf is it has no children.

Searching §

23 57 62 123 159 194 215 274 287 384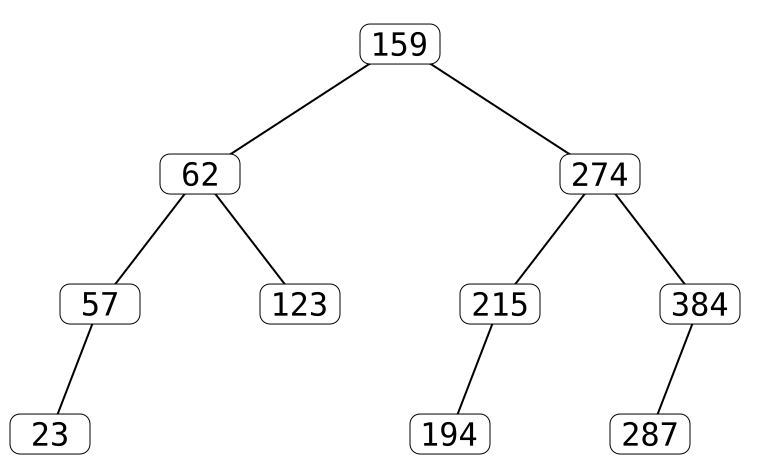

In code (Binary Search) §

struct node {
  node *left;
  node *right;
  int data;
};
 
node *
treesearch (node *n, int *k) {
  if (NULL = n) {
    return NULL;
  }
  else if (k == n.data) {
    return n;
  }
  else if (k < n.data) {
    return treesearch (node->left, k)
  }
  else {
    return treesearch (node->right, k)
  }
}

Tree Traversal §

Depth first (inorder or infix):

• left subtree.
• root.
• right subtree.

Depth first (preorder or prefix):

• root.
• left subtree.
• right subtree.

Depth first (postorder or postfix):

• left subtree.
• right subtree.
• root.

Breath first:

• all roots at each level in turn.
• to do efficiently needs the right representation.

Direction of Traversal §

All traversals can be right to left instead.

• R->L inorder is the inverse of L->R inorder.
• R->L preorder is the inverse of L->R postorder.
• R->L postorder is the inverse of L->R preorder.