Search and Fitness

Definition of a Search Problem §

---

For some problems we need to search for a solution from a (usually) very large number of possibilities, search problems.

The solution spaces for many every day problems can be very, very large, too large to search exhaustively.

It might not find the optimal solution, but it will give a good solution in reasonable time.

We often need special search algorithms known as heuristics.

Heuristics §

---

It is a “rule of thumb” or some loose set of guidelines.

• It might find a solution, but not guaranteed.
• For example: getting out of a maze by keeping your hand against the maze wall.

Usage of domain knowledge in the search process speeds up the search process.

In AI, these are used to improve the performance of methods, in our case, search methods:

• Expert knowledge.
• Common sense.

Search Problems §

---

Many problems can be thought of as searching through candidate solutions to find one that is optimal.

• Systematically search through potential solutions without considering all of them.

We need some way to evaluate the fitness of the candidate solutions:

• Optimal = the fittest = the best etc…

Need to compare solutions and see which of the solutions are better or worst.

Also some sense of the adjacency (similarity) of solutions (or neighbourhood).

Fitness §

---

In order to search for a solution, we must be able to compare potential solutions.

• For example, is solution $s_1$ better than solution $s_2$?
  • Thus we have the concept of fitness.

We must derive a function (the fitness/objective function) that maps a solution to a value that rates how good the solution solves the problem in hand.

We either try and maximise or minimise fitness.

A slight change in solution quality should result in a corresponding change in the fitness.

• Solution quality goes down -> fitness goes down (decreases).
• Solution quality goes up -> fitness goes up (increases).

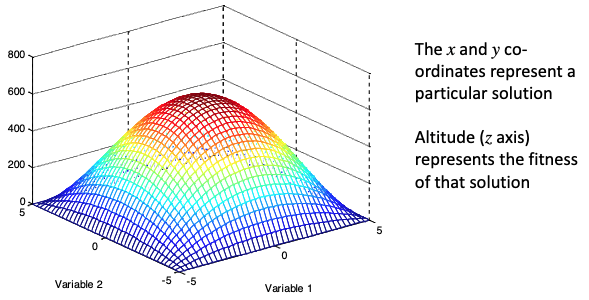
Fitness Landscapes §

---

It can be helpful to think of searching a landscape of solutions where:

• The x and y co-ordinates represent a particular solution.
• Altitude (z axis) represents the fitness of that solution.

This leads to the analogy that we wish to search for or climb peaks (or descend…).

The collection of all possible solutions can be considered as a high dimensional space, called the search space or fitness landscape.

Often, some concept of distance between solutions exists and some concept of how “good” each point in the search space is (fitness/objective function).

Techniques exist to map a high dimensional space to a two dimensional space, so we can plot the space/landscape.

Smooth and regular spaces are easy to search:

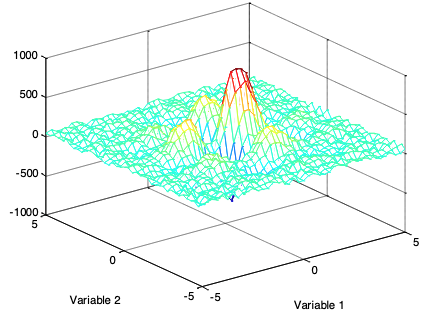
Irregular spaces are difficult to search:

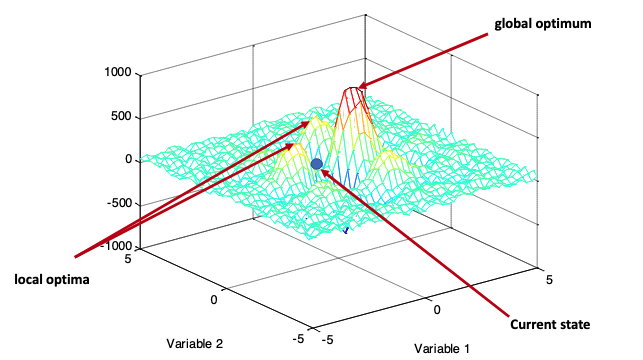
Global and Local Optima §

---

The global optimum is the point or points in the search space with the best objective function evaluation.

A local optimum is the point or points in a subset or section of the search space with the best objective function evaluation.

Note that the subset or section of the search space in question may contain the global optima.

Many search techniques can find local optima, but get “stuck” at them and cannot move on to find the global optima.

Representation §

---

When we are trying to solve a search based problem, we need a way to represent a potential solution.

This is usually a mathematical and/or data structure based way of describing the solution to a problem.

A good representation:

• Should be a one to one mapping.
• No redundancy.
• No ambiguities.
• All potential solutions should be represented.

The Scales Problem §

---

Given $n$ objects of various weights, split them into two equally heavy piles (or as equal as possible).

We have $n$ weights that are $W=[w_1,w_2,...,w_n]$ in weight, $w_i>0$.

We want to divide them into two equals piles in weight, or as equal as possible.

We are going to work with the general case, not a specific set of given weights, we want to solve the problem for any W.

We first look to see if there is a simple or standard method to solve the problem, for this example problem there is not.

We need to:

• Design a representation.
• Construct a fitness function.
• Apply a heuristic search method.

Representation §

---

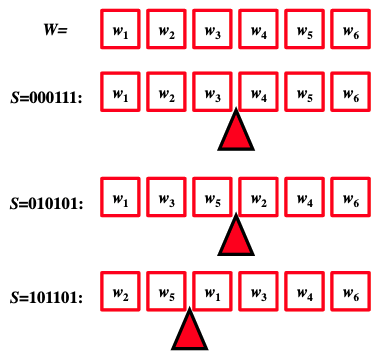
Each weight ($w_i$) is either on the left hand side or the right hand side.

Given that we have $n$ items into two piles/sets we could use a binary representation.

We present a solution as an n length binary string (or array/vector/list…) where:

• A zero (0) in position $i$ means that weight $i$ is on the left side of the scales.
• A one (1) in position $i$ means that weight $i$ is on the right side of the scales.
• This can represent all possible allocations.
• We will refer to this string as $S$ and each bit as $s_i$.
• If $s_i=0$ then weight $i$ is on the left hand side pan/scale.
• If $s_i=1$ then weight $i$ is on the right hand side pan/scale.

Fitness §

---

We now need to design an appropriate fitness function.

This function should score how good a solution (a binary string) is at solving our problem.

What’s the aim of the problem?

• Equal balancing (or as near as possible).

Balanced would be when the sum of the weights on the left hand side (LHS) of the scales equals the sum of the right hand side (RHS).

The worse this difference is the worse our solution is at solving the problem.

What is the best fitness?

• Zero (balanced).

How about the worst fitness?

• When all the weights are on either the left hand side or right hand side.

Thus, this is a minimisation problem.

• Let L = Sum of LHS weights.
• Let R = Sum of RHS weights.
• Fitness = $|L-R|$

The fitness function will take two parameters:

• A potential solution - binary string of length $n$.
• A set of weights - a real vector/array of length $n$.

It will then return a real number.

Each weight $w_i$ will either be added onto the left hand side L or the right hand side R.

So we can iterate through each weight adding it to L or R depending on what side of the scales the representation specifies the weight is on.

Example §

---

So imagine we have five weights:

• $W=1,2,3,4,10$.
• $w_1=1,w_2=2,w_3=3,w_4=4,w_5=10$.

Some example fitness (F):

• $S=11111$

  • $L=0,R=1+2+3+4+10=20,F=|0-20|=20$

• $S=10101$

  • $L=2+4,R=1+3+10,F=|6-14|=8$

• $S=01010$

  • $L=1+3+10=14,R=2+4=6,F=|14-6|=8$

• $S=11110$

  • $L=10,R=1+2+3+4=10,F=|10-10|=0$

What’s next? §

---

We have a representation.

We have a fitness function.

We now want to search through a number of possible $S$ until we find the best one.

• For example, when $F(S,W)=0$.
• Or as close to zero as possible.

We therefore need to apply an appropriate heuristic search method:

• Random Mutation Hill Climbing, Stochastic Hill Climbing, Random Restart Hill Climbing, Simulated Annealing, Genetic Algorithms, Particle Swarm Optimisation, Tabu-Search, Iterated Local Search, Evolutionary Programming, etc…