Genetic Algorithms belong to a family of techniques that are inspired from evolution theory.
- Each gene is a binary digit.
- A chromosome is a string of genes.
A solution to a problem is encoded as a chromosome. The encoding is called a representation and it covers the whole search space.
The fitness function rates how good a solution to a chromosome is.
The population is the number of chromosomes “alive” at any one time. Generations is the number of times breeding has occurred.
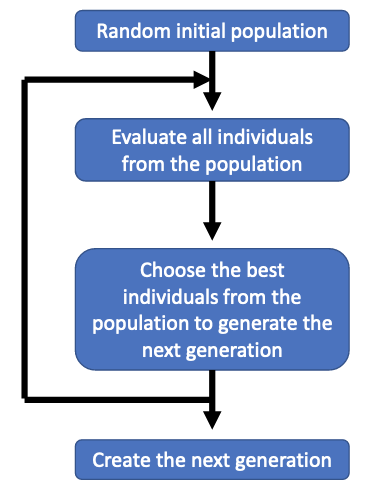
Overview
- Create a population of random chromosomes.
- Each chromosome is scored using a fitness function.
- Create a new generation through genetic operators called selection, crossover and mutation.
- Repeat until we get the best solution.
Parameters
- NG: Number of generations (100, 1000)
- PS: Population size (10, 100)
- CP: Crossover probability (50%-100%)
- MP: Mutation probability (0.1%-10%)
- n: the number of bits (genes) making up each chromosome.
Pseudo-Code
- Holland’s GA Algorithm:
Input: The GA parameters: NG, PS, CP, MP and n
The Fitness Function
1) Generate PS random Chromosomes of length n
2) For i = 1 to NG
3) Crossover Population, with chance CP per Chromosome
4) Mutate all the Population, with chance MP per gene
5) Kill off (or fix) all Invalid Chromosomes
6) Survival of Fittest, e.g. Roulette Wheel
7) End For
Output: The best solution to the problem is the Chromosome
in the last generation (the NGth population) which
has the best fitness value
Crossover
- Analogous to recombination or breeding.
Typically it means that genetic material from two parents are combined to create children.
Various crossover operators:
- One-point crossover.
- Uniform crossover.
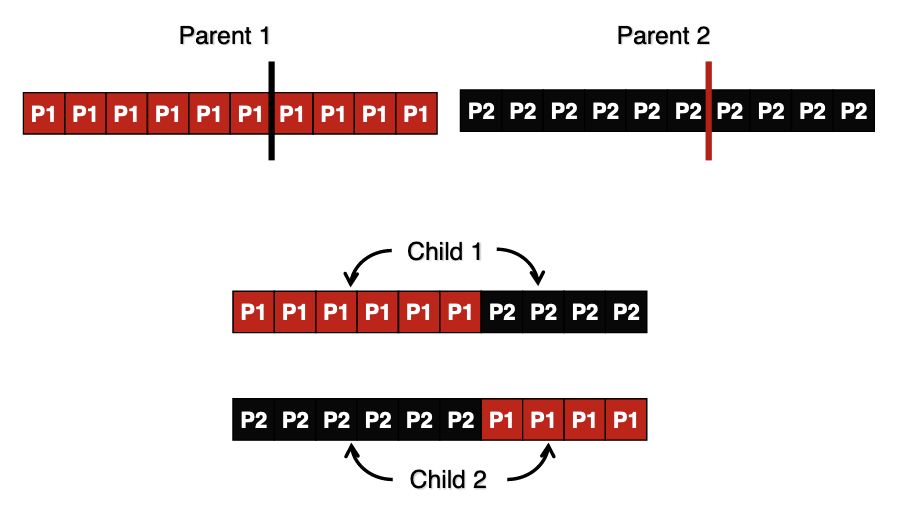
One-Point Crossover
- Chromosomes (with n genes) move to the crossover pool with CP chance.
- Each are randomly paired up (A and B).
- Two children are created (C and D).
- A random number p between 2 and n-1 is generated for each parent pair.
- 1..p of A become 1..p of D.
- p+1..n of A become p+1..n of C.
- 1..p of B becomes 1..p of C.
- p+1..n of B become p+1..n of D.
- Put them in the population.
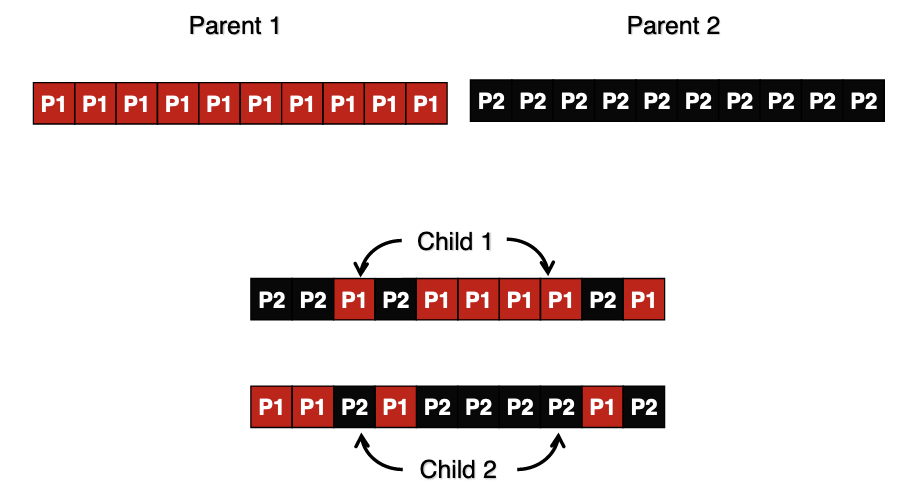
Uniform Crossover
It is more powerful.
- For each gene, there is a 50% chance that child C gets the gene from parents A and a 50% chance that it is from parent B.
- Child D gets the gene that child C does not.
Mutation
Small random tweak of the gene to get a new solution.
It allows the genetic algorithm to explore more of the search space and avoid falling into local minima.
Selection
Roulette
It aims to retain the best performing chromosomes (solutions) from one generation to the next.
It forms a new population, equal in size to the original.
The chance of a chromosome surviving is proportional to it’s fitness vs the total of the others.
Knapsack Problem
Given n items, each with a weight and a value, determine the items to include so that the total weight is less than or equal to a given limit and the total value is as large as possible.