Asymptotic Analysis

---

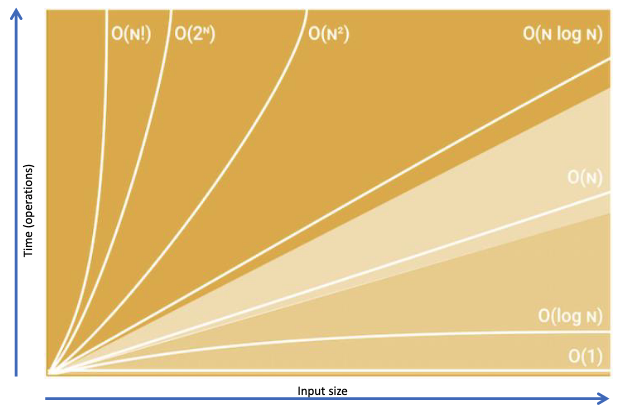
The asymptotic analysis of an algorithm determines the running time in Big O notation.

To perform the asymptotic analysis:

• We find the worst-case number of primitive operations executed as a function of the input size, $T(n)$.
• We express this function with Big O notation.

Big O notation defines an upper bound of an algorithm (worst-case).

The runtime in terms of how quickly it grows is relative to the input, as the input gets larger.

More info here (Time Complexity).

Big-O Runtime Analysis §

---

1. Find out the input and what $n$ represents.
2. Calculate the primitive operations of the algorithm in terms of $n$.
3. Drop the lower-order terms.
4. Remove all constant factors.

Example §

---

The algorithm ArrayMax executes at most $T(n)=8n-5$ primitive operations.

We say that algorithm ArrayMax runs in $O(n)$ time.

Since constant factors and lower-order terms are eventually dropped, we can disregard them when counting primitive operations.

We do not have to be 100% accurate as long as we get he powers of $n$ correct.

Rank from Fast to Slow §

---

Before	After
$T(n)=n^4$	$T(n)=lo{g}_n\equiv O(lo{g}_n)$
$T(n)=nlo{g}_n$	$T(n)=n\equiv O(n)$
$T(n)=n^2$	$T(n)=n+2n\equiv O(n)$
$T(n)=n^{2}lo{g}_n$	$T(n)=nlo{g}_n\equiv O(nlo{g}_n)$
$T(n)=n$	$T(n)=n^2\equiv O(n^2)$
$T(n)=2^n$	$T(n)=n^{2}lo{g}_n\equiv O(n^{2}lo{g}_n)$
$T(n)=lo{g}_n$	$T(n)=n^4\equiv O(n^{2}lo{g}_n)$
$T(n)=n+2n$	$T(n)=2^n\equiv O(2^n)$

Polynomial Time §

---

An algorithm is solvable in polynomial time if the number of steps required to complete the algorithm for a give input is $O(n^k)$ for some non-negative integer $k$, $n$ being the complexity of the input.

The Classes of Algorithms §

---

Problems are divided up into a number of classes (classifications):

• Computable:
  • Problems that can be solved using a computer.
  • For example: $f(x)=x+1$.
• Non-computable:
  • Problems that cannot can be solved using a computer.
  • For example: Halting Problem.

P and NP problems §

Algorithms are divided up into a number of classes (classifications):

• P problems:
  • Solved in a reasonable amount of time (polynomial time).
  • For example: multiplication and sorting.
• NP problems:
  • Difficult to solve in a reasonable amount of time but easy to verify the solution.
  • Problems involving decision making.
  • Important class of problems, for example job scheduling, circuit design and vehicle routing.

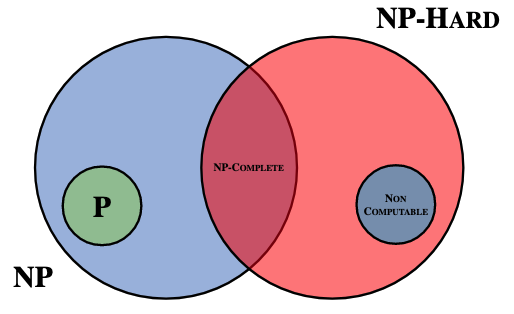
• NP-hard problems:
  • Very, very difficult to solve problems, which cannot be done in a reasonable amount of time.
  • They are very difficult to verify in polynomial time.
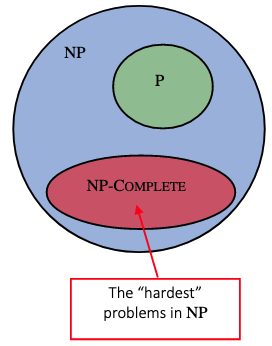
• NP-complete problems:
  • The hardest problems in NP set.
  • Complexities greater than polynomial time.
  • Verifiable in polynomial time.
  • No polynomial-time algorithm is discovered for any NP-complete problem.
  • Nobody was able to prove that no polynomial-time algorithm exist for any of the problems.

If a polynomial time algorithm is found for any problem in NP-complete then every problem in NP can be solved in polynomial time.

More info here (P vs NP problems).

Examples §

---

• The travelling salesperson problem.
• Finding the shortest common superstring.
• Checking whether two finite automate accept the same language.
• Given three positive integers a, b, and c, do there exist positive integers (x and y) such that $a{x}^2+b{y}^2=c$.